√ おうぎ形 面積 求め方 208059-おうぎ形 面積 求め方 ���ワザ
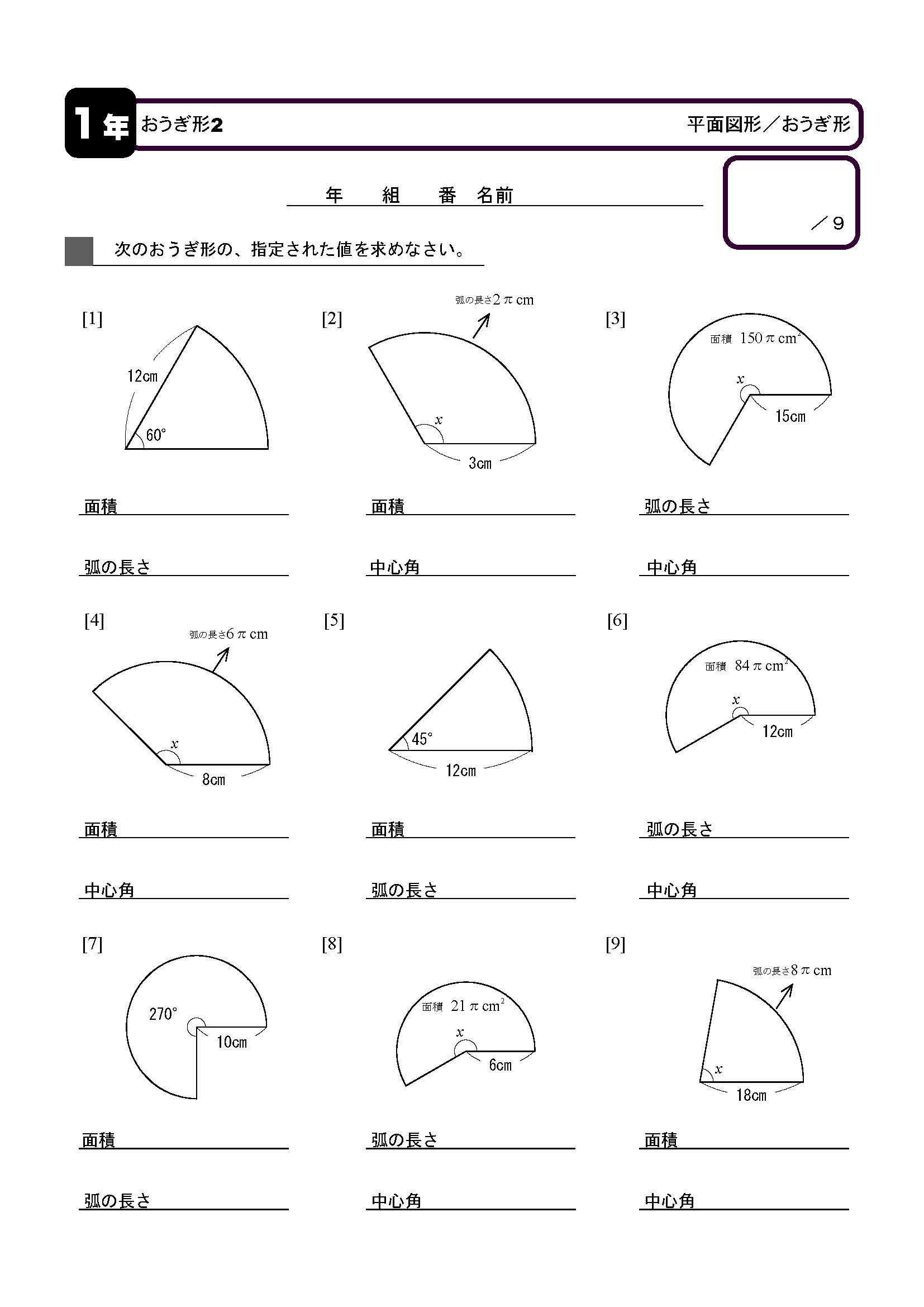
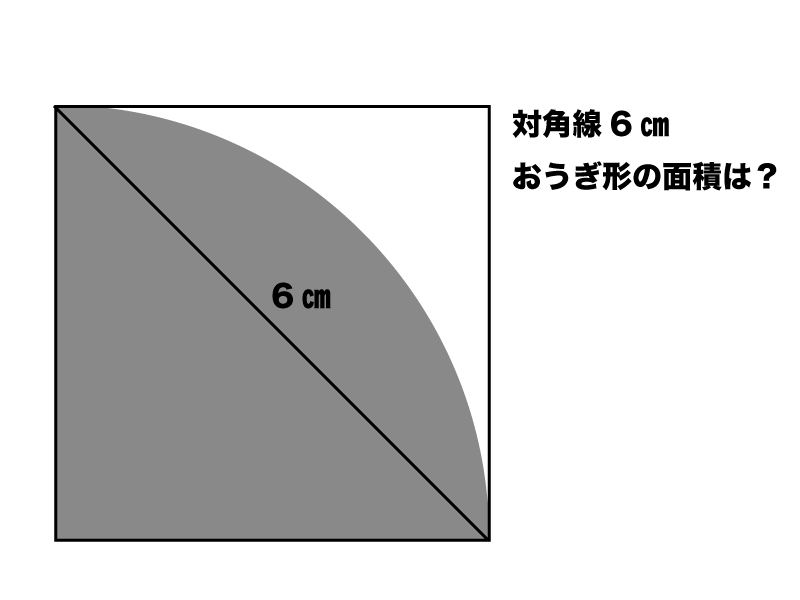
まずはこの図から「円」の面積を求めてみます。 6 × 6 × 314 = 円全体の面積 おうぎ形の面積は、 円の1周360°に対して中心の角度が何度かを分数にします。 上記の場合は90°ですから〔90 / 360〕となります。 わかるなら〔1/4〕としてしまってもいいです。 よって上記のおうぎ形の面積は・・・ 6 × 6 × 314 × 90/360 → 9 × 314 = 26 正方形の面積を出す 与えられている情報が対角線しかありままずは、円の面積と円周の求め方をおさらいしましょう。 円の面積 半径 × 半径 × 円周率 ( 314) ですが、中学では、半径 = r , 円周率 = π として、次のように表します。 r × r × π = π r 2 円周 直径 × 円周率 ( 314) ですが、中学では、半径 = r , 円周率 = π として、次のように表します。 2 × r × π = 2 π r ※ π をかく順番は数字の後、文字の前になります。おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時にどれくらいの割合なのか ということ。 たとえば中心角が 270° 270 ° 、 180° 180 ° 、 90° 90 ° 、 45° 45 ° といったおうぎ形は元の円と比べるとそれぞれ 3 4 3 4 、 1 2 1 2 、 1 4 1 4 、 1 8 1 8 の大きさになっているのは明らか
扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典
おうぎ形 面積 求め方 裏ワザ
おうぎ形 面積 求め方 裏ワザ-演習問題で理解を深める! (1)半径が3㎝の円周の長さと面積を求めなさい。 (1)解説&答えはこちら (2)半径が8㎝の円周の長さと面積を求めなさい。 (2)解説&答えはこちら (3)半径が10㎝の円周の長さと面積を求めなさい。 (3)解説&答えはこちら 円の公式が身についたら 次はおうぎ形の公式を確認していきましょう!数学 扇形の 半径 と 面積 が分かっている場合、 どうやって扇形の弧の長さをもとめればいいんでしょうか



扇形 面積の計算 計算サイト
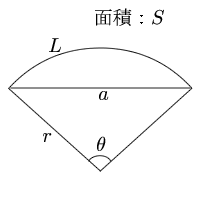
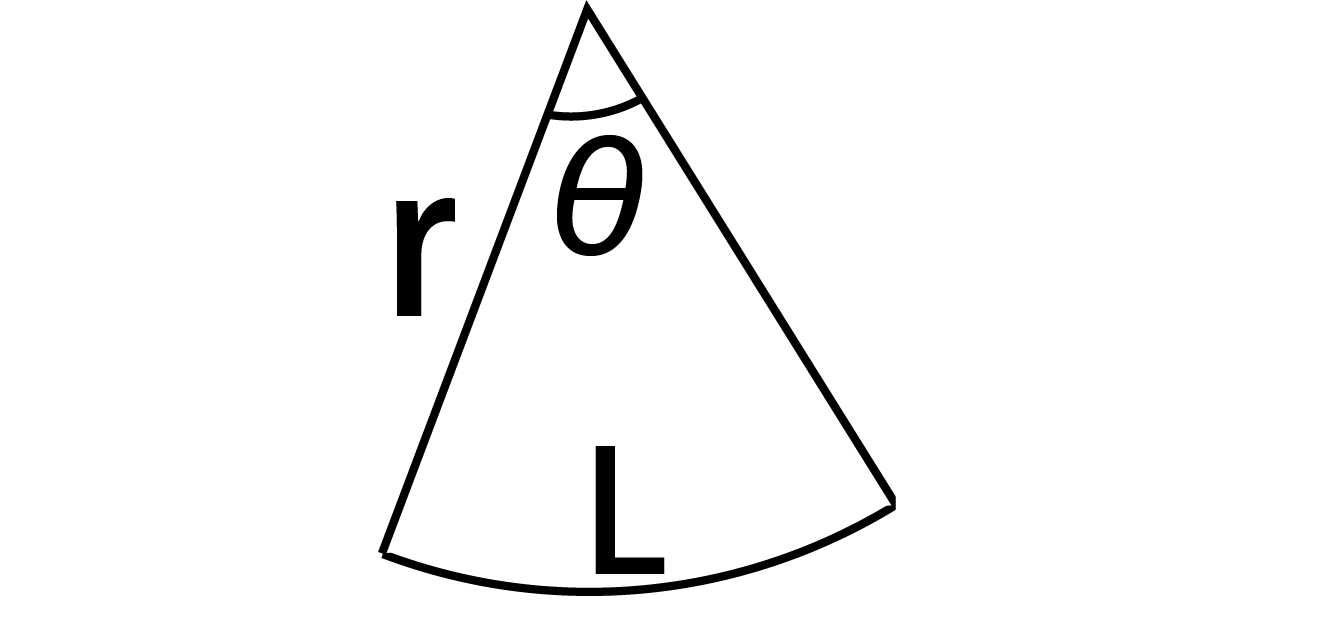
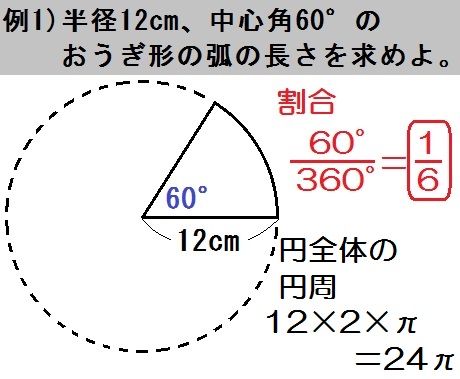
① おうぎ形の弧の長さ = 直径 × π × 中心角 360° より 弧の長さ = 18×π× 64 360 = 16 5 π 答 16 5 π cm ② おうぎ形の面積 = 半径 × 半径 × π × 中心角 360° より 面積 =9×9×π× 64 360 = 72 5 π 答 72 5 π cm 2 確認 次の問いに答えよ。 半径6cm, 中心角30°のおうぎ形の弧の長さを求めよ。 数学 数学 超裏ワザ! ! おうぎ形の面積の求め方 表紙 1 2 3 公開日時 21年12月29日 17時19分 、ということでしたので解説してみます。 まず、扇形の 「面積」 や 「弧の長さ」 を求める考え方ですが、「母線 x を半径とする円の面積 or 円周」 から 「おうぎ形の中心角の割合」 を掛けることで求めることができます。 母線 x と中心角 θ が分かっている場合、おうぎ形の弧の長さを求める式は次のようになります。 この式を利用して、母線 x と弧の長さ z が分かっていて中心角 θ
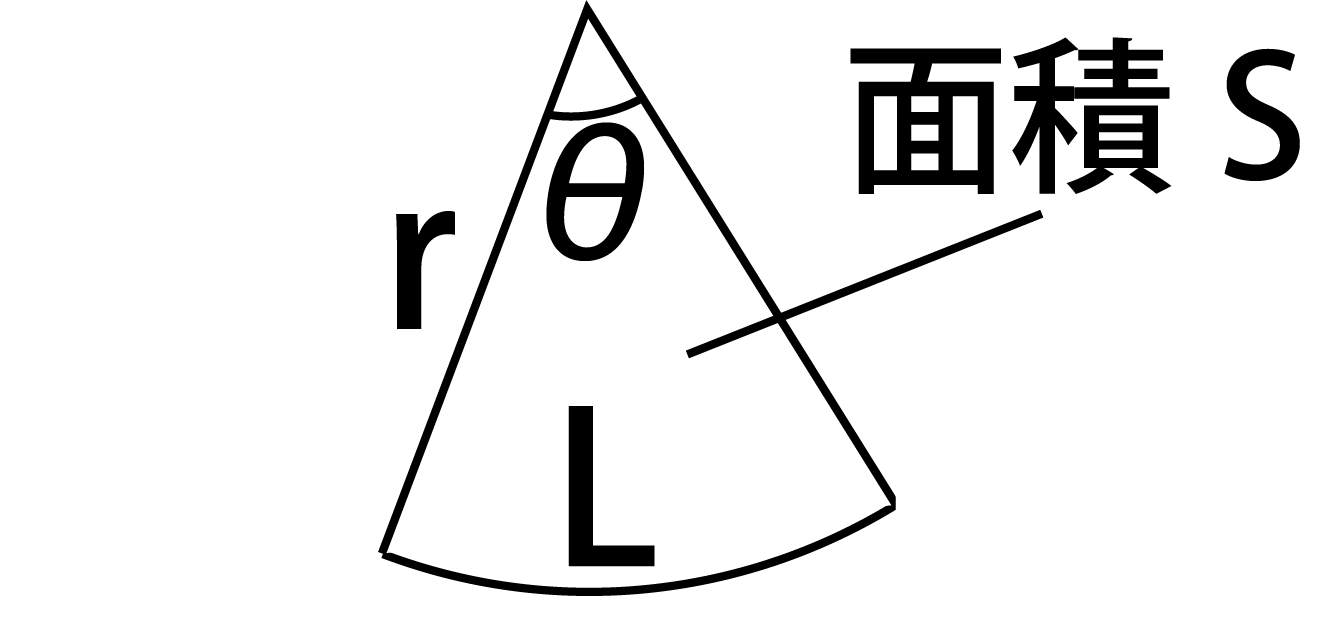
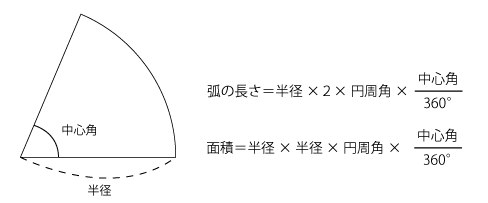
1年 おうぎ形の面積|数学イメージ動画集|大日本図書 おうぎ形の面積を考えてみます。 弧の長さが l l ,半径が r r のおうぎ形を細かく切ると平行四辺形のようになります。 おうぎ形の面積は,底辺が 1 2l 1 2 l ,高さ r r の平行四辺形の面積と同じに 扇形(おうぎ形)の面積の求め方 扇形の面積を求めるときには次の公式を使います。 扇形の面積 =半径×半径×円周率× ※扇形の面積は、円の面積に をかけることで求めることが出来ます。 ※円周率は、小学校ではふつう314を使います。おうぎ形の面積を求める公式 面積=円の面積×中心角の割合 半径5cm、中心角36度のおうぎ形の面積は何cm 2 ? (円周率はπとする) 中心角の割合を求める 36/360 = 1/10 円の面積を求める (半径×半径×円周率) 5 × 5 × π = 25π おうぎ形の面積を求める 25π × 1/10 = 25π cm 2 弧の長さを求める場合も考え方は同じで、中心角から割合を求め、円の円周に割合を掛けて弧の長さを求めます。 円周を
まとめ:扇形の弧の長さの求め方、おっけい! さいごに復習しておこう。 扇形の弧の長さLの求め方は、 L = 2πr×α/360 だったね?? ピザのカロリーを計算するように、扇形の弧の長さを求められれば大丈夫。 時間があったら、扇形の面積の求め方も復習し円が、中心角が 360° 360 ° のおうぎ形ということです。 円を 360 360 等分すると、中心角が 1° 1 ° のおうぎ形になります。 この面積は 円の面積 × 1 360 1 360 この中心角 1° 1 ° のおうぎ形が 75 75 個集まると、その面積は 円の面積 × 1 360 ×75 × 1 360 × 75 これつまりこの問題は (1)まずおうぎ形・三角形の面積を求め, (2)その差し引きで潰れた部分を求め, (3)最後に色のついた部分を求める,と進めていけばいいわけです。 ではこの手順に従って各部分を計算していきます。 まずおうぎ形ですが,この図形の半径



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
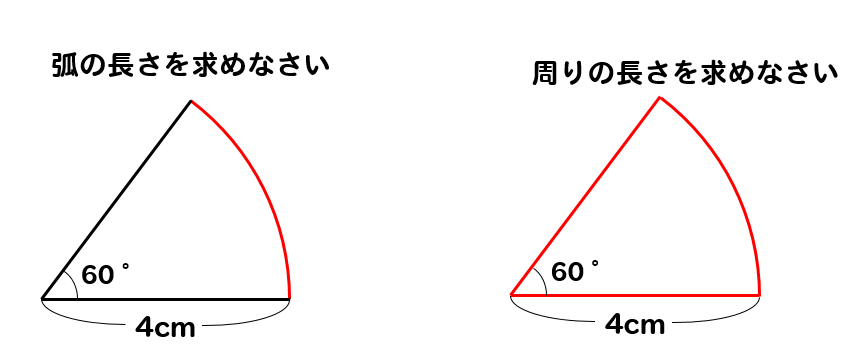



おうぎ形 注意 周りの長さを求める公式を解説 数スタ
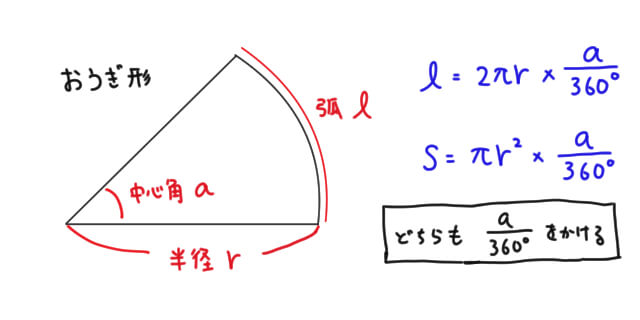
扇形の面積の求め方・公式 それでは扇形の面積の求め方を考えてみましょう。 半円の面積は、もとの円の面積の半分になりますね。 同様に、円を6等分してできた扇形の面積は、もとの円の面積の6分の1です。 半径が 3 で、中心角が 1 3 π のおうぎ形の場合、面積は、 1 2 × 3 2 × 1 3 π = 3 2 π となります。 まとめておきましょう。 弧度法を使ったおうぎ形の弧の長さと面積 半径が r で、中心角が θ のおうぎ形の弧の長さを l とし、面積を S とすると、次が成り立つ。 l = r θ S = 1 2 r 2 θ = 1 2 r l おわりに ここでは、弧度法を使って、おうぎ形の弧の長さや面積を求める方法を見ました。 シンプル こちらも π π を使うことで円と同様にスッキリ表すことができます。 半径 r r 、中心角 α° α ° のおうぎ形の弧の長さ ℓ ℓ と面積 S S 弧の長さ ℓ ℓ : ℓ = 2πr× α 360 ℓ = 2 π r × α 360 面 積 S S : S = πr2 × α 360 S = π r 2 × α 360 つまり、おうぎ形の弧の長さと面積は中心角の大きさ α α に比例します。 実はおうぎ形の面積を求める裏技があります。 S = 1
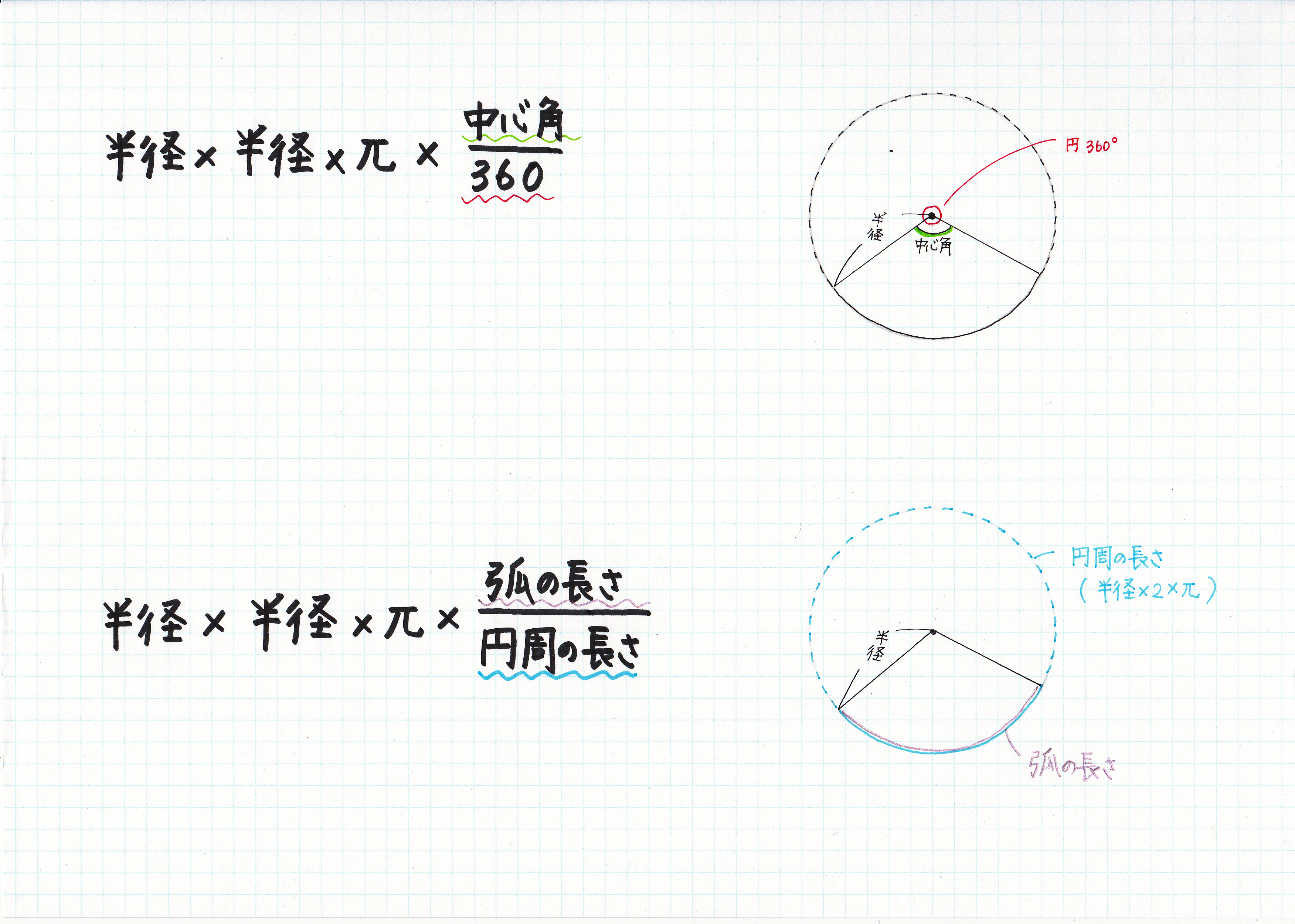



おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学
これがポイント! このおうぎ形を含む円の面積は、 6×6×3.14 で求められますね。 (先週のヒント: 円の面積は半径×半径×3.14 ) このおうぎ形は中心角が 60° という事ですから、 360° のうちの 60° の大きさ。 360÷60=6ですから、円をちょうど 6等分この問題のポイント ・おうぎ形の孤の面積は、次の公式を使って求めることができます。 おうぎ形の半径をr、中心角をaとすると、面積Sは次の式で求めることができます。 S = π r 2 × a 360 おうぎ形の面積は、半径と中心角の大きさが判れば求めることができます。 もし、おうぎ形の孤の面積が、なぜこの公式で求めることができるのかについて、疑問に思った時単元:おうぎ型の中心角の解き方 今日はおうぎ形の中心角を求め方について学習していこう。 それでは早速問題を解いていきましょう。 半径9㎝、弧の長さが6n㎝のおうぎ形の中心角を求めなさい。 え-っと。 弧の長さが分かっているので,おうぎ形の




扇 おうぎ 形の面積を求める公式と弧の長さの求め方



おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook
扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。図をもとに式を立てよう! おうぎ形については、 中心角が90° だから、 (おうぎ形1つの面積)=3×3×π×90/360 (三角形の面積)=3×3×1/2 これらを利用すれば、求める ラグビーボールの面積 が求められるね。 練習の答え円とおうぎ形の面積は,どうやって求めるの 無断複製・転載・翻訳を禁ず ©GAKKEN B




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
おうぎ形の面積の求め方 \ (1\)、半径\ (r\)と中心角\ (a\)を公式\ (\pi r^2\times\frac {a} {360}\)に代入する \ (2\)、半径\ (r\)と弧の長さ\ (l\)を公式\ (\frac {1} {2}lr\)に代入する おうぎ形の面積の公式 おうぎ形の面積の公式は次のとおり。 おうぎ形の面積の公式 \ (1\)、おうぎ形の面積\ (\hskip2pt=\pi r^2\times\frac {a} {360}\) ・ \ (r\)は半径、\ (a\)は中心角 ・ おうぎ形の弧の長さ、面積、中心角の求め方と公式 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は 180^\circ 180∘ 、さらに半分切りとれば中心角は 90^\circ 90∘ になります。 ケーキを半分に切ったり、三分の一にしたりするときを想像円周や面積については、以下の公式によって計算します。 円周 = 直径 × 314(円周率) 円の面積 = 半径 × 半径 × 314(円周率) ただ中学数学では、円周率として314を使いません。314は正確な数値ではなく近似値に過ぎないからです。
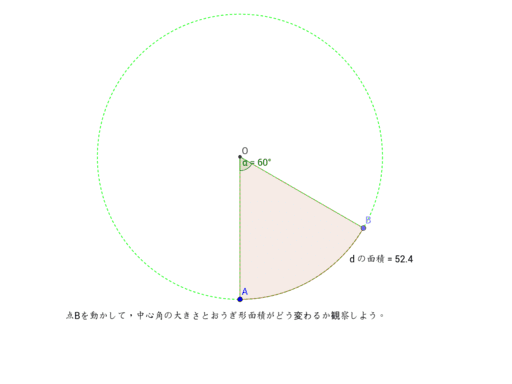



中心角とおうぎ形 Geogebra




扇形の半径の求め方 計算のやり方をイチから解説していくぞ 中学数学 理科の学習まとめサイト
a×d=b×c という形になるね。 これをおうぎ形に使ってみよう。 おうぎ形で比例式を使うときは、調べたいおうぎ形と半径が同じ円を考えましょう。 つまり、 この2つで考えるということですね。 作る比例式は、以下になります。 小6算数「円の面積とおうぎ形」の問題 どこよりも簡単な解き方・求め方 「円」を等分(同じ大きさに分ける)して細かく細かくしていって並べかえると「ほとんど長方形」になります この長方形の「たて=円の半径」「よこ=円周の半分(半径×314)」なので「円の面積=半径×半




扇形 面積の計算 計算サイト
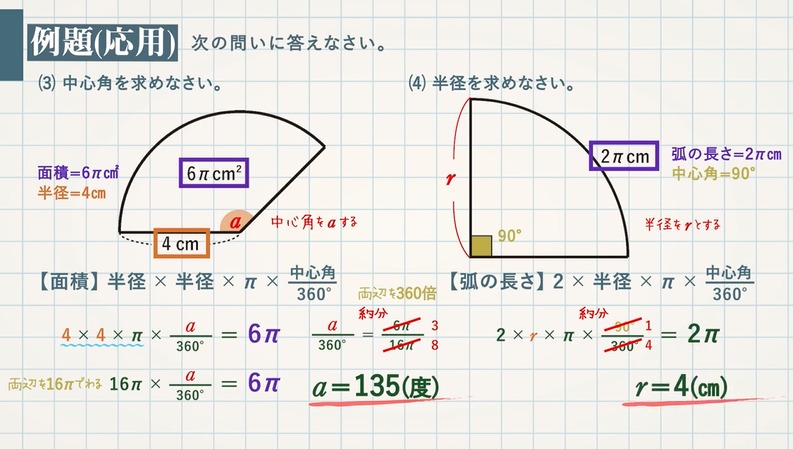



おうぎ形まとめ 弧と面積の求め方 教遊者



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ




おうぎ形まとめ 弧と面積の求め方 教遊者




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




おうぎ形の弧の長さと面積の求め方 チーム エン
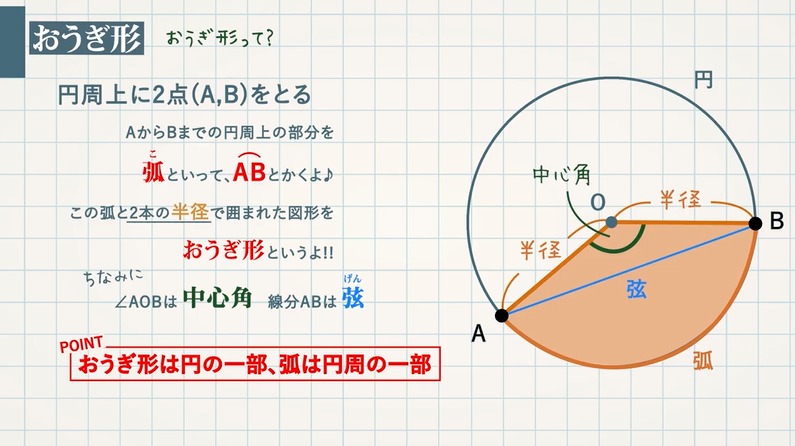



おうぎ形まとめ 弧と面積の求め方 教遊者




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
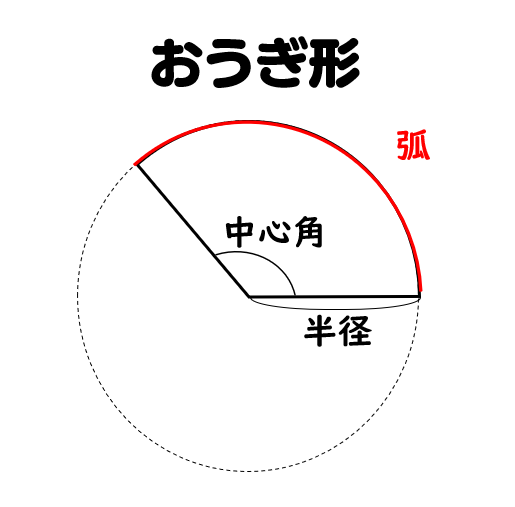



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
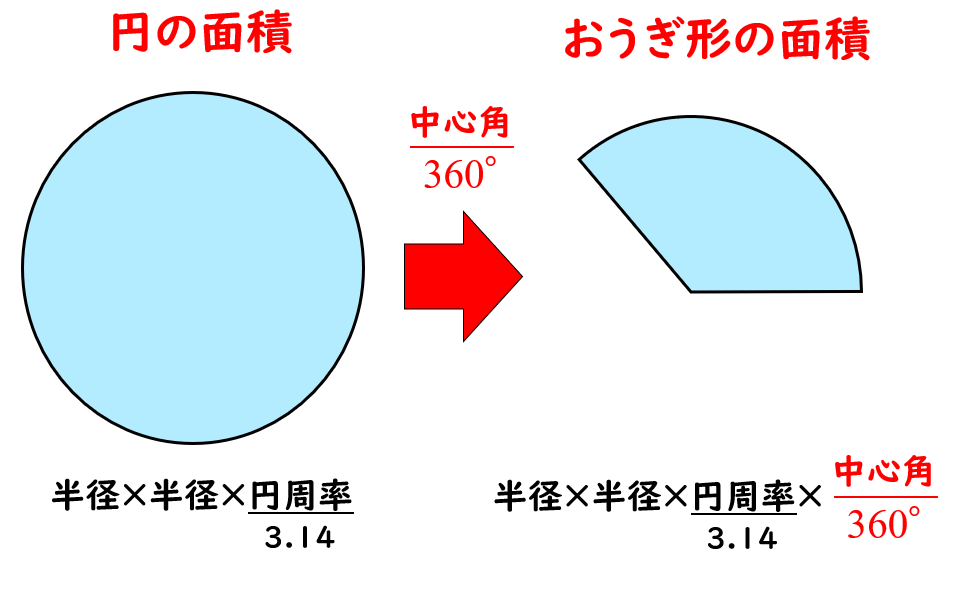



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




おうぎ形の面積 高さ からなる立体の解き方 高校入試予想問題の解 数学 教えて Goo



中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ




公式オンライン アウトレット 円とおうぎ形の平面図形 小学 算数 A1272a19 激安の通販 Www Cfscr Com
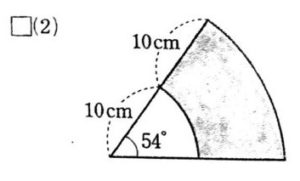



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




おうぎ形の中心角の求め方 Youtube




おうぎ形 面積 中心角 弧の長さの求め方 公式と裏ワザも紹介 トムラボ




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか



円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル




円 扇形 の面積 周や弧の長さの公式 数学fun




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張



モノマナビ研究所




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
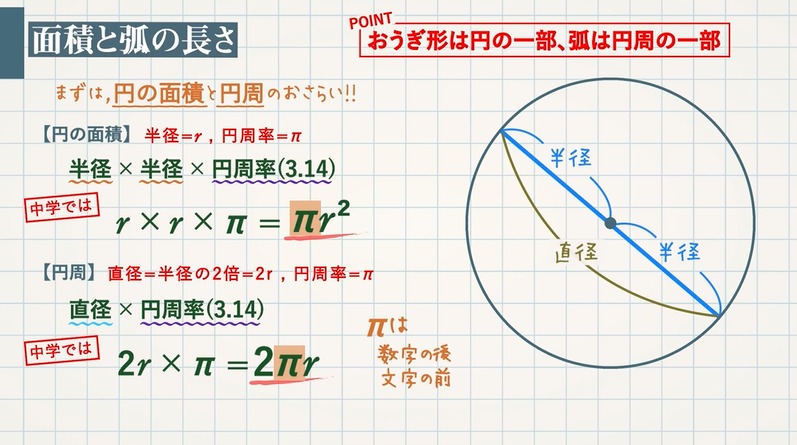



おうぎ形まとめ 弧と面積の求め方 教遊者
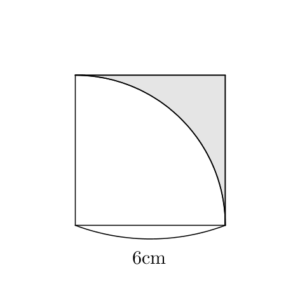



標準 おうぎ形と正方形の面積 なかけんの数学ノート




円 扇形 の面積 周や弧の長さの公式 数学fun




中1数学 おうぎ形の公式 例題編 映像授業のtry It トライイット




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
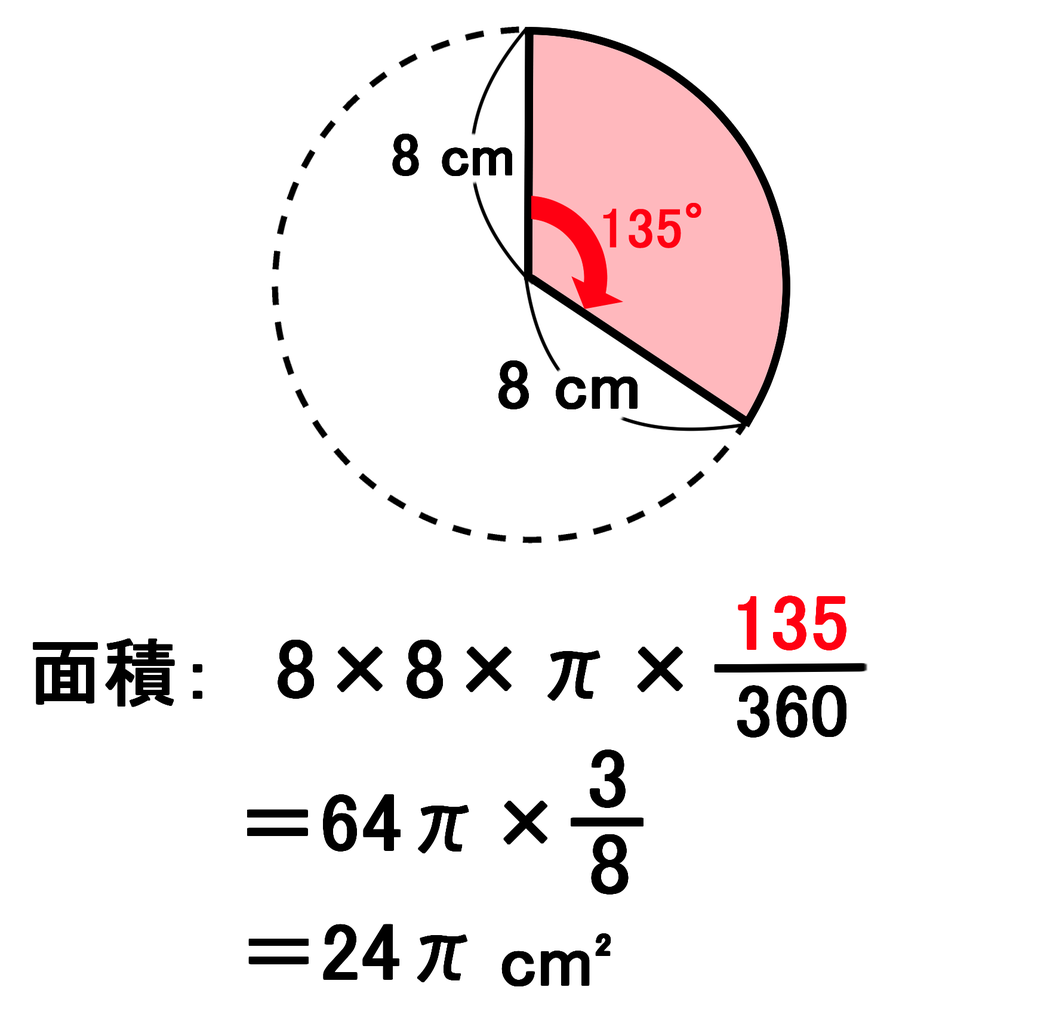



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
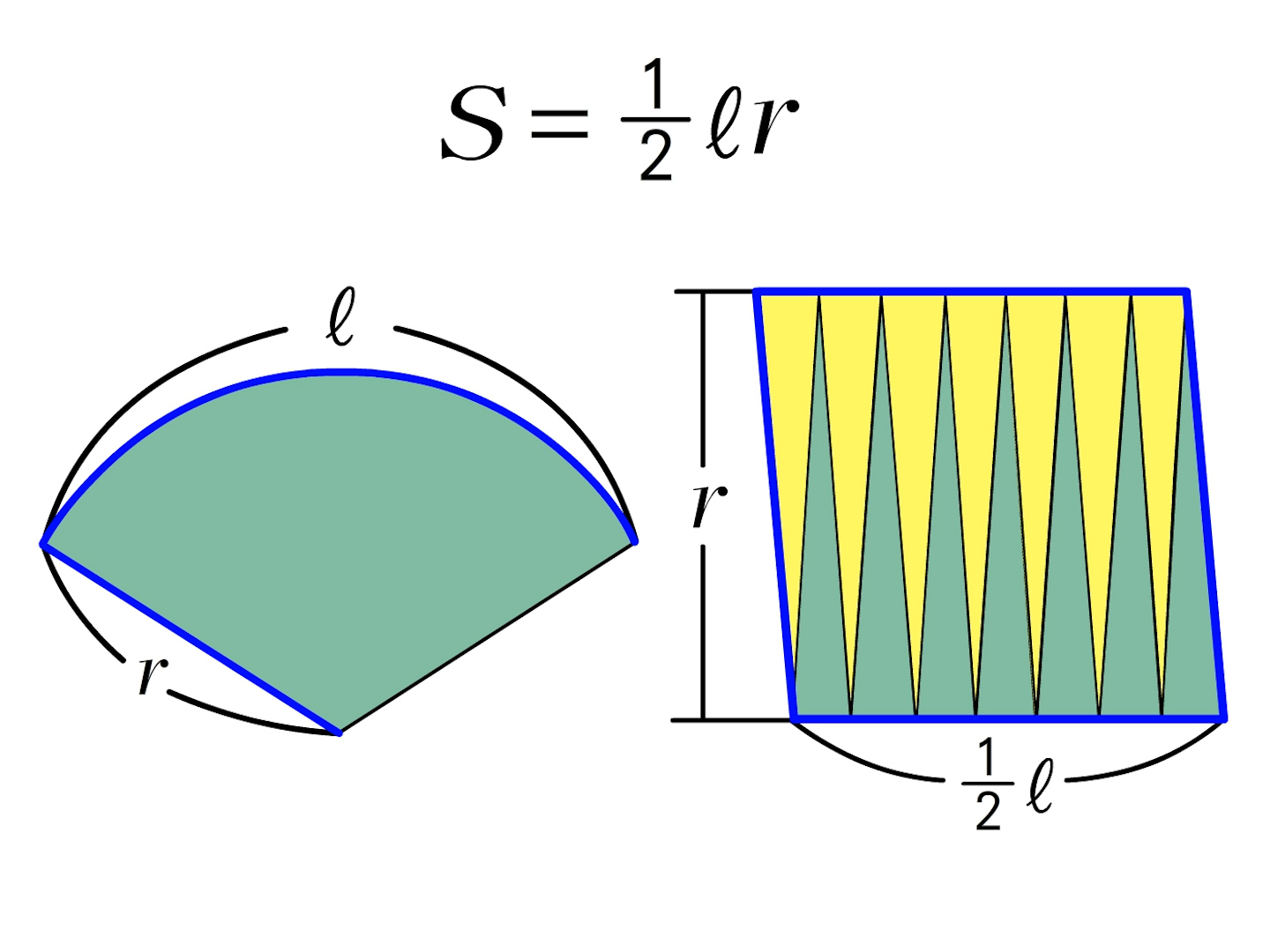



1年 おうぎ形の面積 数学イメージ動画集 大日本図書
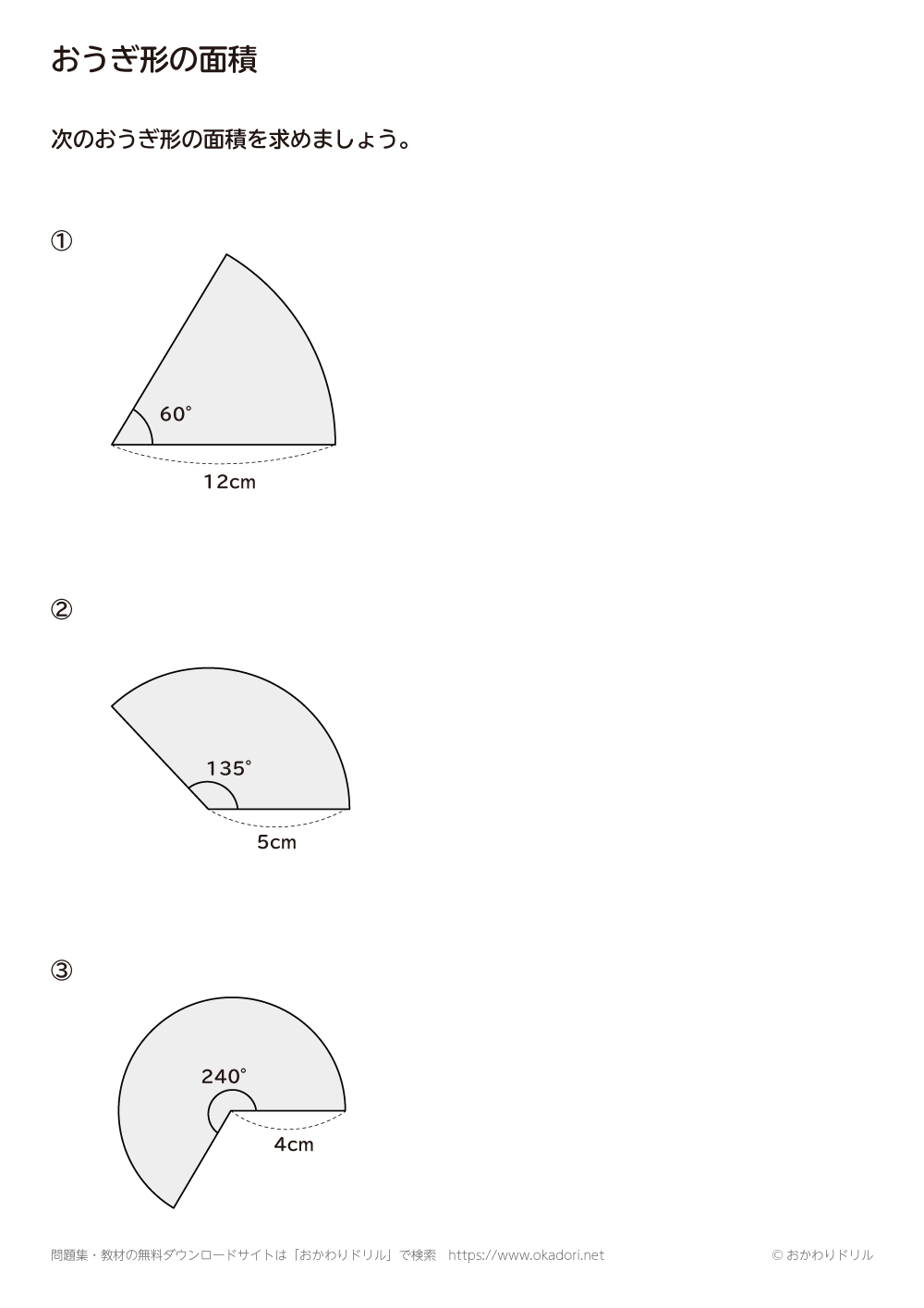



中学1年生 数学 無料問題集 おうぎ形の面積 1 おかわりドリル



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube
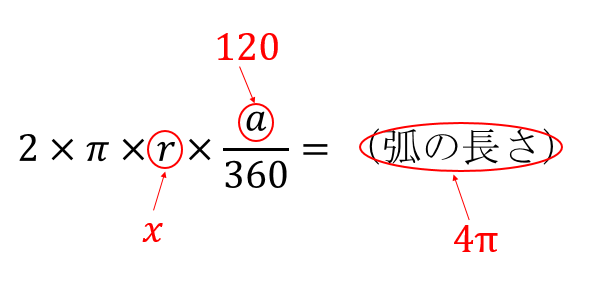



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




算数 本当に 分かる という事 おうぎ形の面積その1 エース学院



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典



中学数学 円すいに関する練習問題 トルテン




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ



円とおうぎ形 中学受験準備のための学習ドリル




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
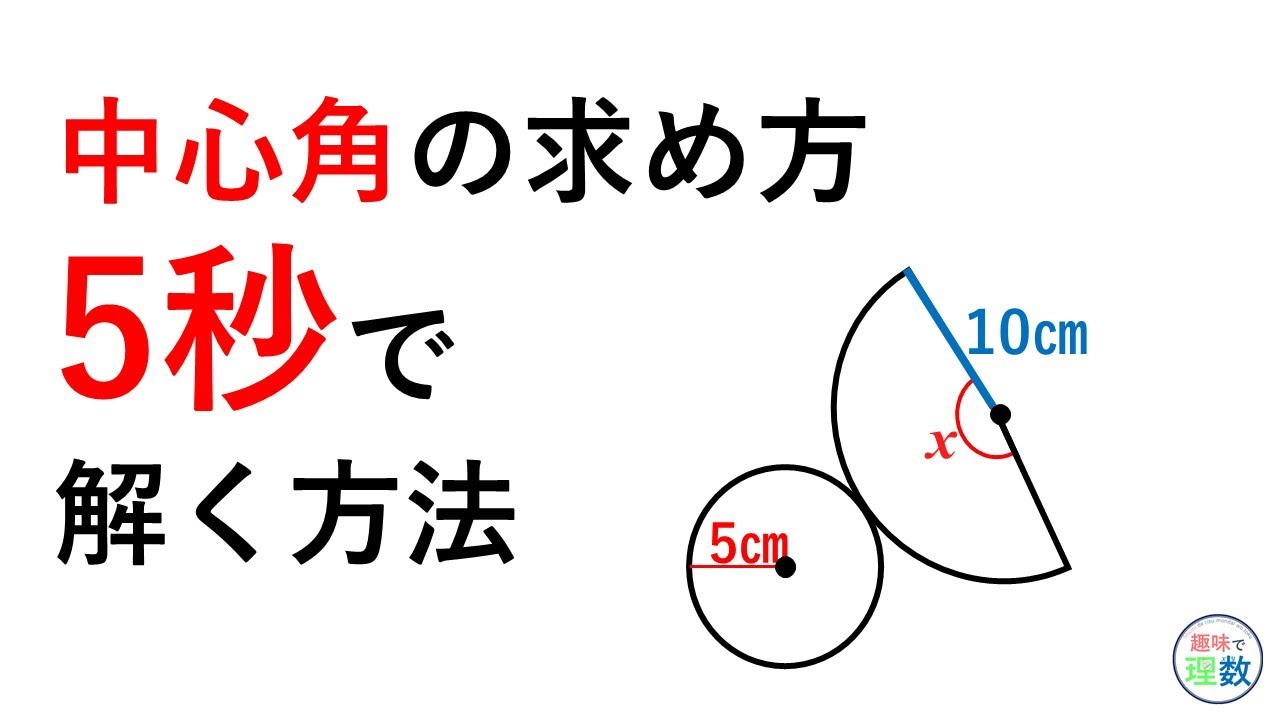



おうぎ形の中心角の求め方 Youtube




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



おうぎ形の面積の公式 算数の公式




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




Download Qikeru 学びを Images For Free




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube



正方形の中のおうぎ形の面積計算 受験算数入門




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
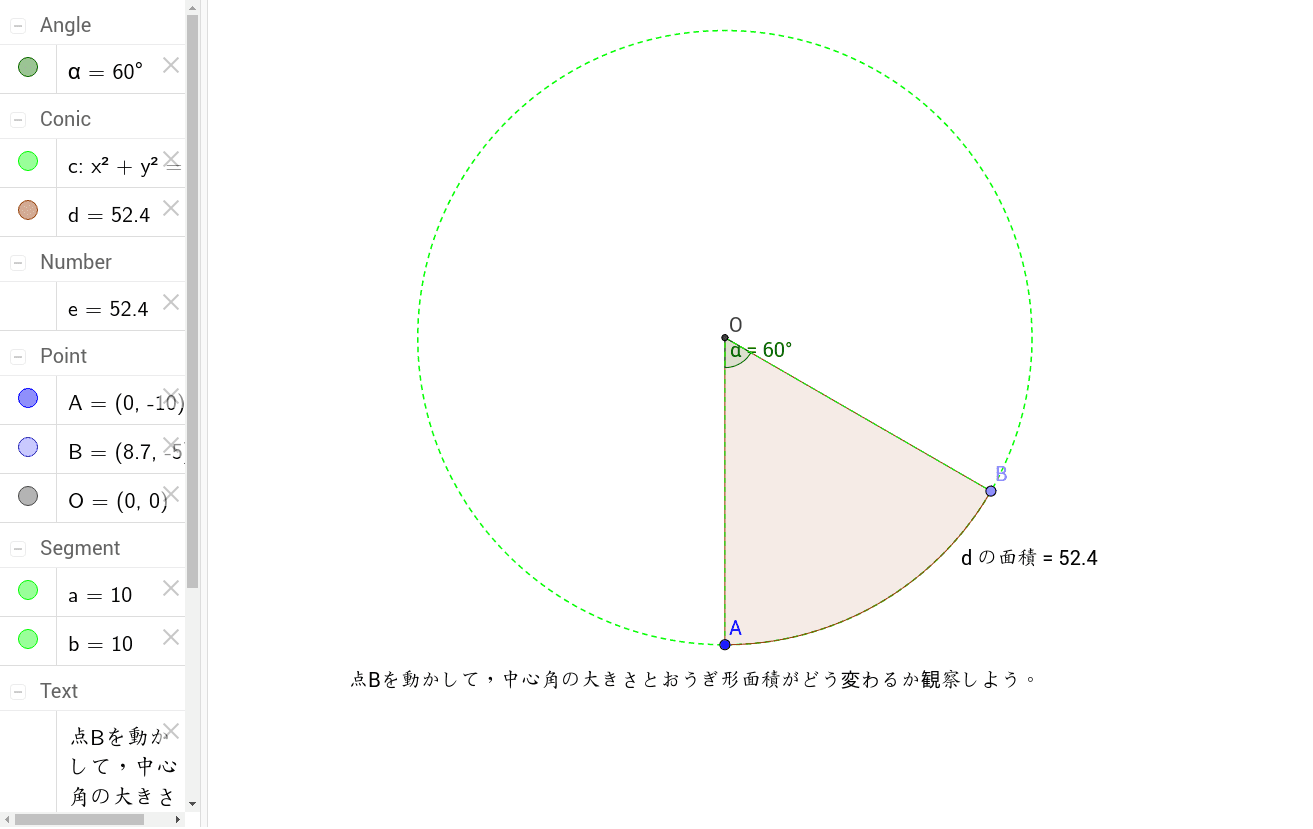



中心角とおうぎ形 Geogebra



中学数学 平面図形 のコツ 円とおうぎ形




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




扇形の面積の求め方 公式と計算例
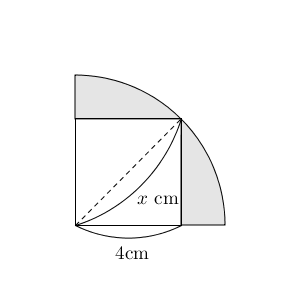



応用 おうぎ形と正方形の面積 なかけんの数学ノート
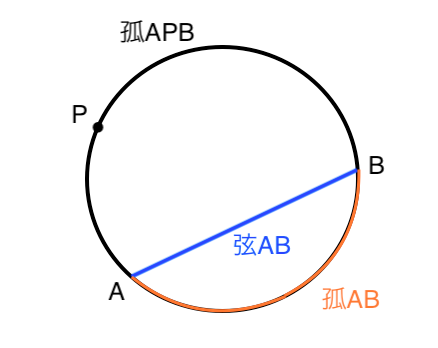



まずはここから おうぎ形について 超基本 苦手な数学を簡単に




円 扇形 の面積 周や弧の長さの公式 数学fun
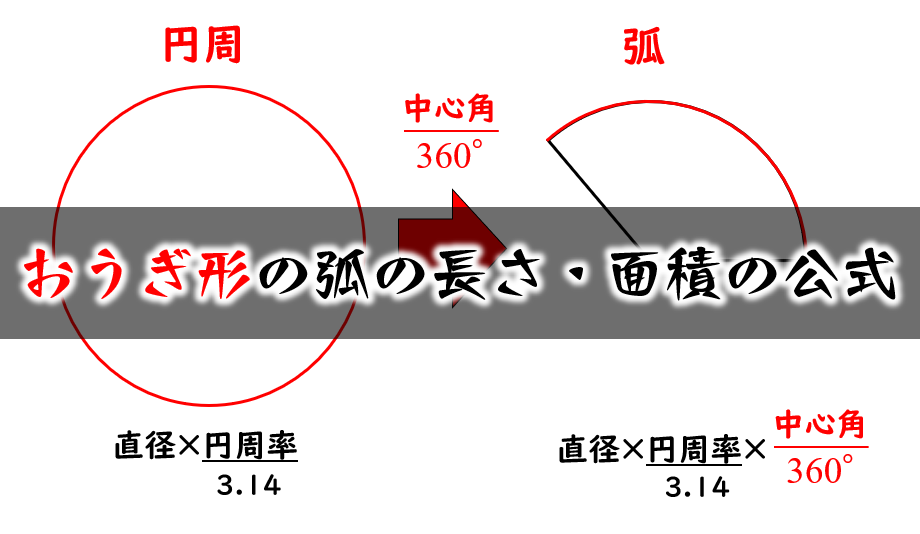



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



3




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




公式オンライン アウトレット 円とおうぎ形の平面図形 小学 算数 A1272a19 激安の通販 Www Cfscr Com




公式オンライン アウトレット 円とおうぎ形の平面図形 小学 算数 A1272a19 激安の通販 Www Cfscr Com




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



3
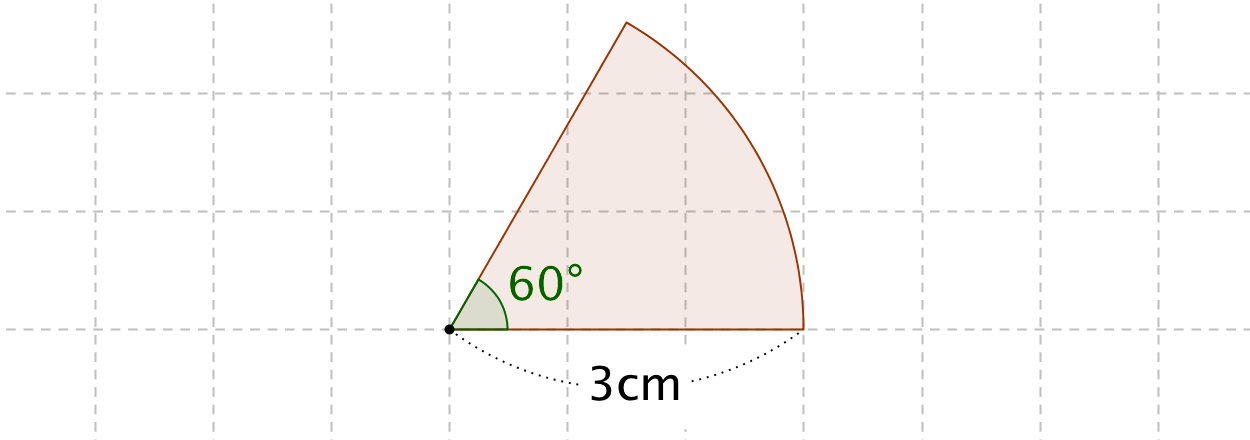



おうぎ形の面積の公式 算数の公式




おうぎ形まとめ 弧と面積の求め方 教遊者




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
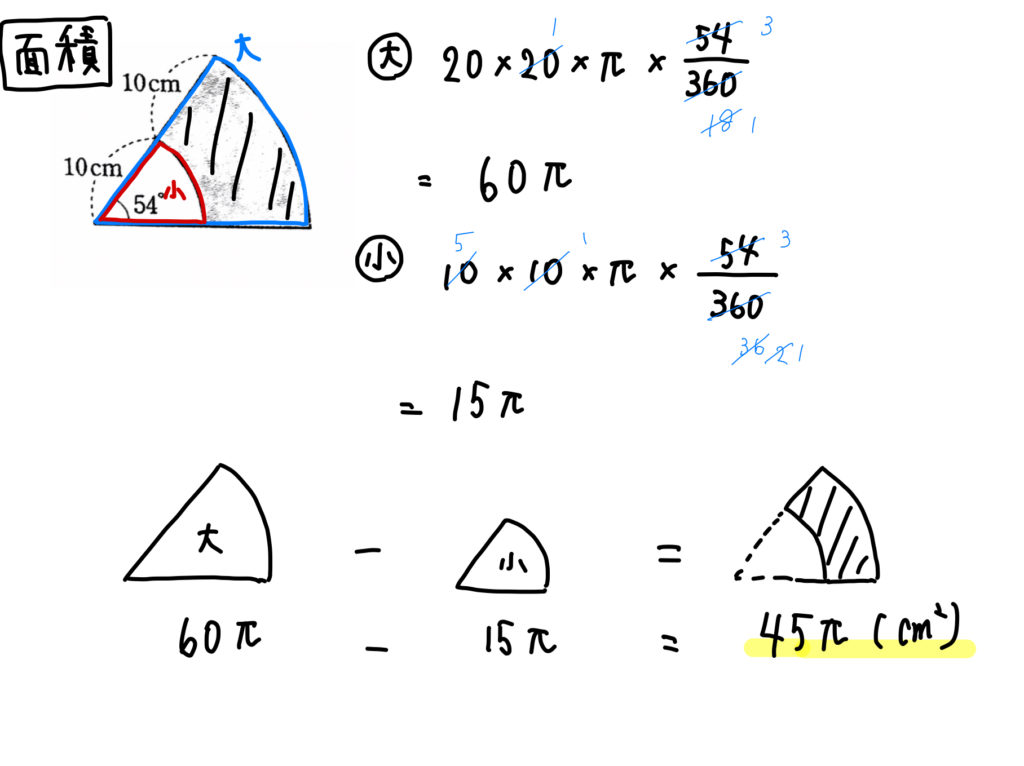



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ



1




おうぎ形面積の超簡単な求め方 合同会社エスキージャパン




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学
コメント
コメントを投稿