いろいろ 三角錐 体積 求め方 高校 299243-三角錐 体積 ���め方 高校

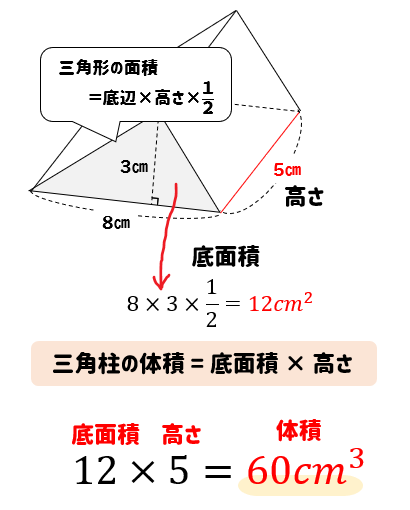
3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ

 高校3年生のめいから質問された問題です。 問題文は下記の図の通りです。 この中で最後の三角錐ompqの体積の求め方が分かりません。 それまでの問いの答えから、 om=3、op=2、oq=4、mp=√7、mq=√13、pq=2√3 と思います。三角錐OAEF＝三角錐AOEF より，求める体積は9cm3 (3)体積を表す式から高さを求める (2)より，三角錐OAEF＝9cm3 と求められているので， 三角錐OAEFの頂点Oから面AEFに下ろした垂線の長さを xとおくと， AEF×x× 1 3 ＝9cm3 となる。 (1)より， AEF ＝ 27 2 だから， 27 2 ×

三角錐 体積 求め方 高校

三角錐 体積 求め方 高校- 1：円錐の体積の求め方 まずは円錐の体積の求め方から解説していきます。 円錐の体積は、「底面積×高さ×1/3」で求めることができます。 ※円錐の体積がなぜ「底面積×高さ×1/3」で求められるのか？ についての証明は特に学習しないので、本記事では円錐の体積の公式の証明は割愛します。 したがって、下の図のように、半径がr、高さがhである円錐の体積Vを 三角錐の体積の求め方 三角錐oabcについて、 OA＝OB＝OC＝5 AB＝4 BC＝5 AC＝6 この三角錐の体積の求め方を教えていただけませんか？？ 底面積は出せるのですが、高さの出し方がどうしてもわかりません。 宜しくお願いします。

高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月

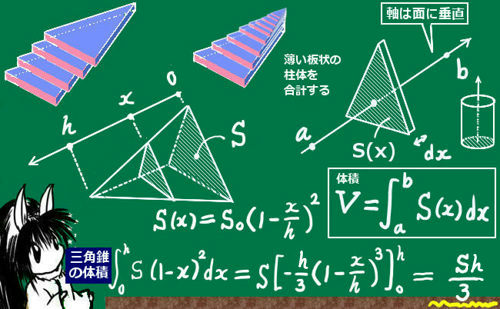
 数学・算数 三角錐の体積の求め方 高校3年生のめいから質問された問題です。 問題文は下記の図の通りです。 この中で最後の三角錐ompqの体積の求め方が分かりません。 それまでの問いの答えから、 質問no 球の体積 体積V = 4 3πr 3 目標：上式で求まる理由を知る（ 積分 等の高校数学を使わずに） はじめに 球の体積 方法①：微小な四角錐を考える 考え方 方法②：カヴァリエリの原理を使う カヴァリエリの原理 錐体の体積が柱体の体積の1／3になることは、高校2年で習う積分法を使うことで説明できます。 (ただし、入試ではやや難問と呼ばれる類に該当するかもしれません) 柱体の底面積を S、高さを h とした場合の体積 V は V = ∫(0→h) S x dx = S h となります。

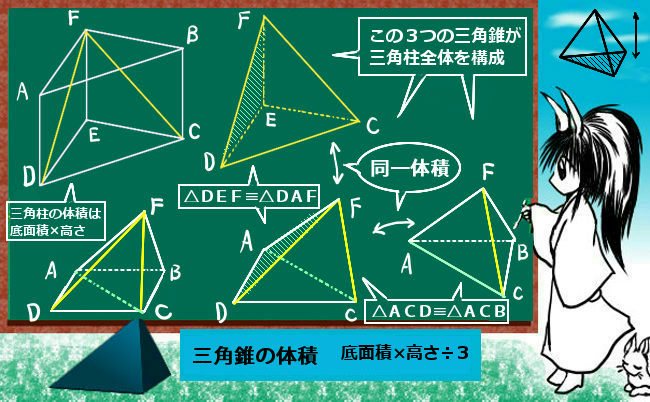
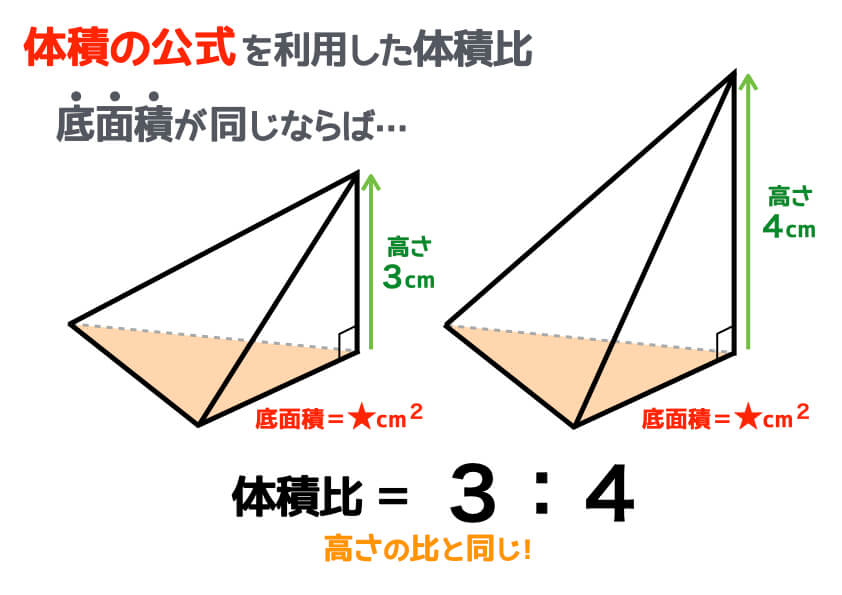
 12三角錐の体積公式 錐の体積 底面積×高さ× (1/3) 三角錐に限らず、錐の体積を求めるには柱との関係で捉えるとよいでしょう。 つまり、柱の体積に3分の1をかければ、錐の体積が求まるという関係にあります。 そして、これを三角錐に関して表現すると、 三角錐の体積 底面積（三角形の面積）×高さ× (1/3) このように表現されることになります。四面体の体積，平行六面体の体積と行列式の関係について。さらに，この公式を応用した美しい式も紹介。東北大の入試が一瞬で解けます。 トップ 新着記事 高校数学の美しい物語 四面体の体積を求める2つの公式with行列式 四面体の体積を求める2つの公式with行列式 レベル ★ 最難関大受験次の三角錐の体積を求めなさい。 三角錐の体積＝底面積 高さ 三角錐の体積を求めるときに気をつけたいのは、 必ず を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず を掛けてください。 また、底面の三角形の面積は、 底面 高さ となることもおさえておきましょう。 すると、計算は次のようになります。 〇

三角錐 体積 求め方 高校のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

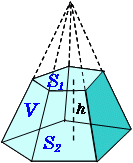
正五角錐の体積の求め方 理系のための備忘録	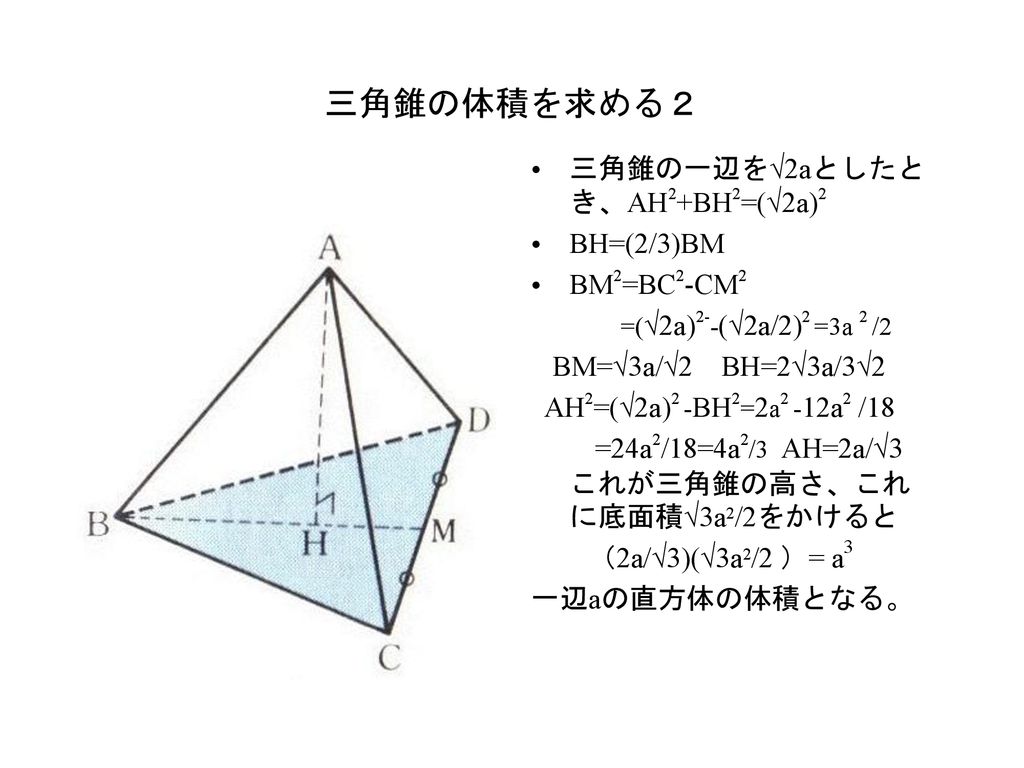正五角錐の体積の求め方 理系のための備忘録	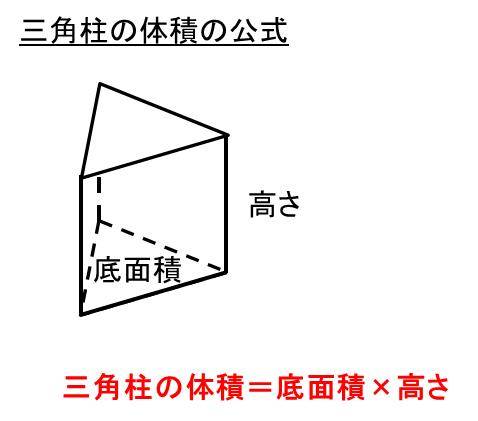正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	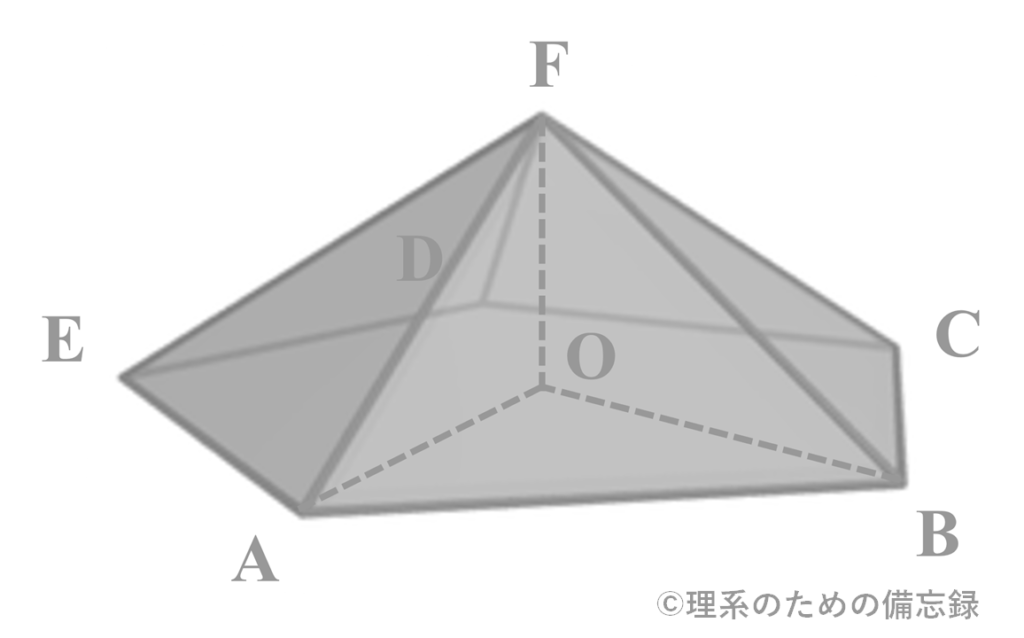正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	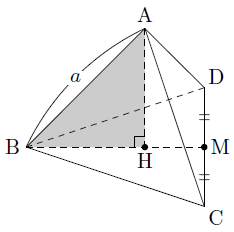正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	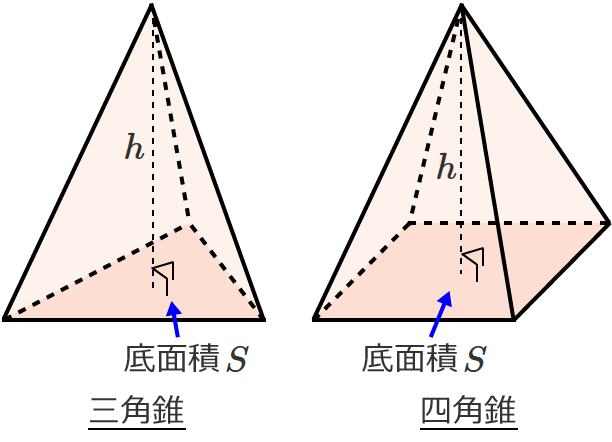正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	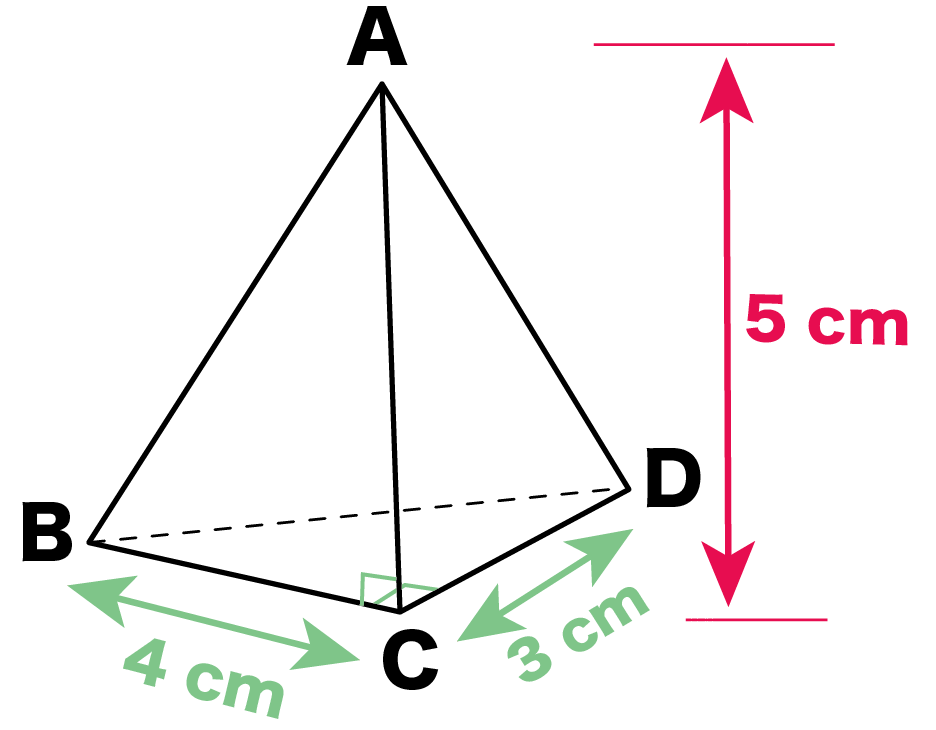正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	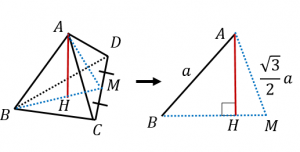正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	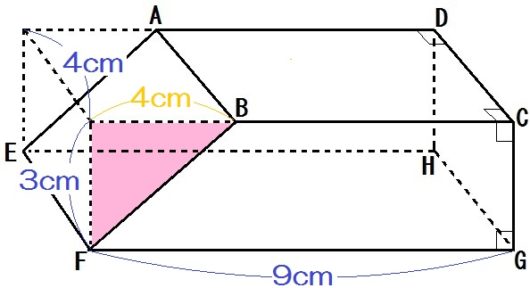正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	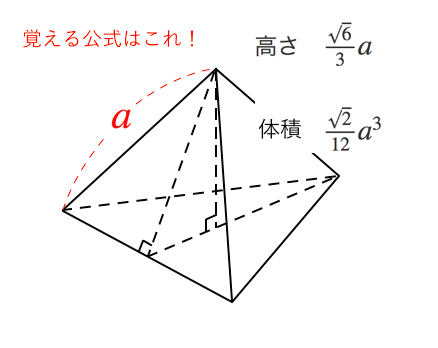正五角錐の体積の求め方 理系のための備忘録
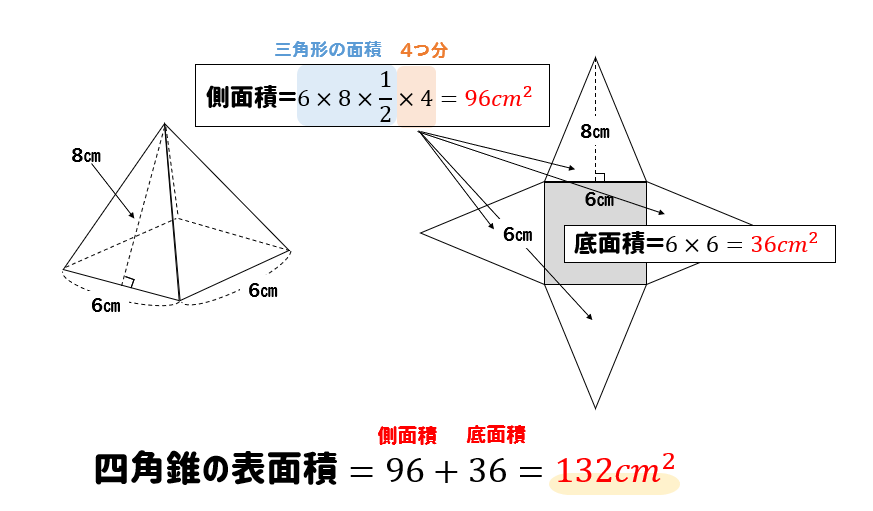正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録
正五角錐の体積の求め方 理系のための備忘録	正五角錐の体積の求め方 理系のための備忘録

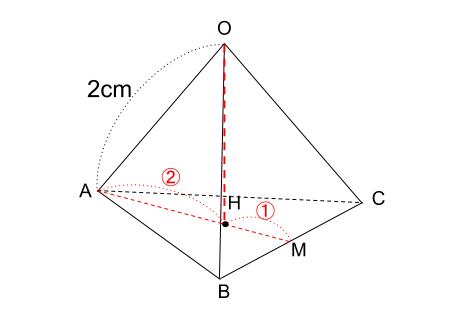
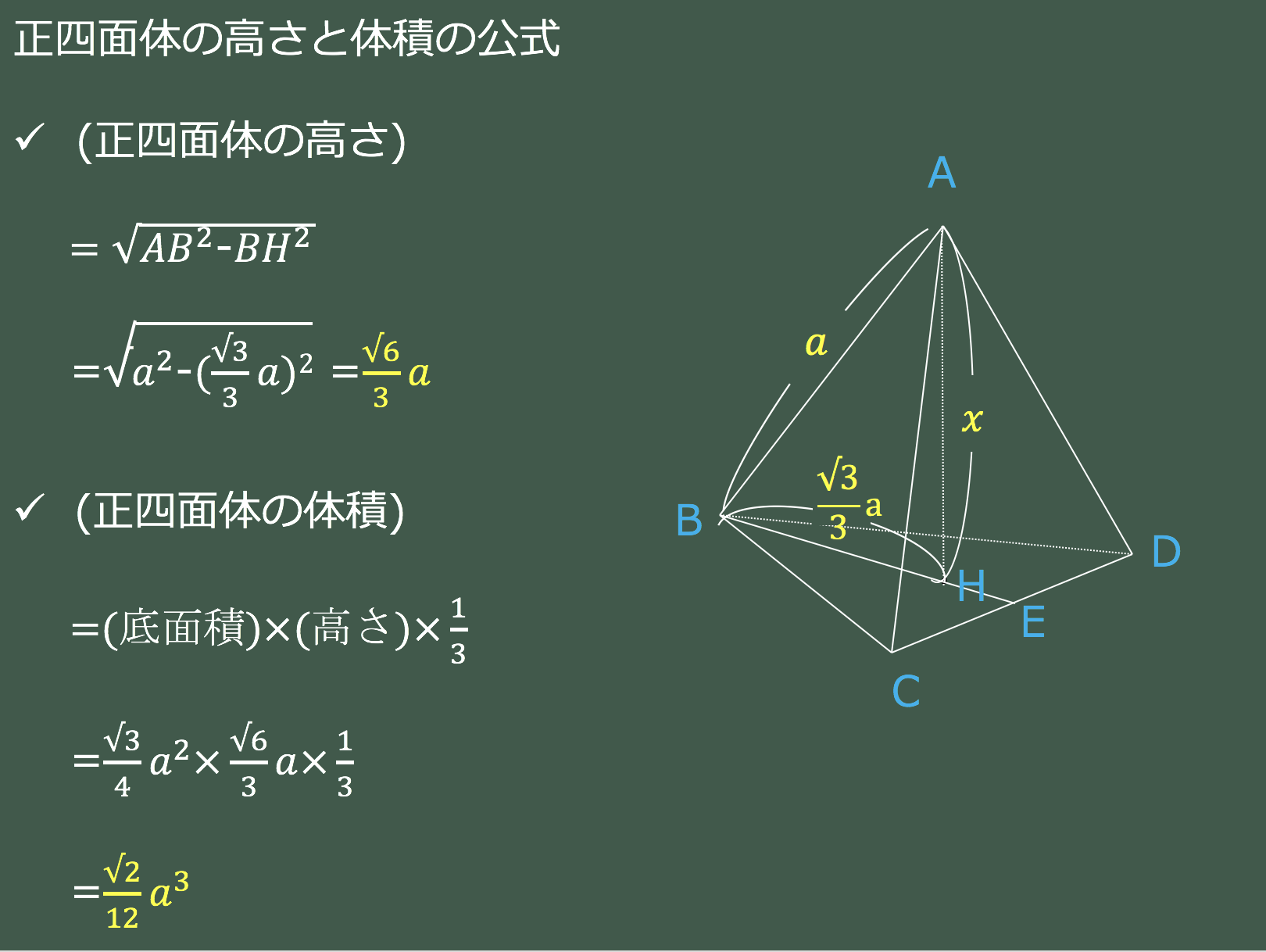
いよいよ体積 ようやく体積を求める準備が整いました。 この正四面体の高さ OH O H は下図のようになっています。 OH O H が何 cm c m なのか求めます。 当然、三角形 OAH O A H に三平方の定理を用います。 AM A M は 1 1 辺が 2cm 2 c m の正三角形の高さなので 三角錐の体積の求め方 三角錐oabcについて、 OA＝OB＝OC＝5 AB＝4 BC＝5 AC＝6 この三角錐の体積の求め方を教えていただけませんか？？ 底面積は出せるのですが、高さの出し方がどうしてもわかりません。 宜しくお願いします。

Incoming Term: 三角錐 体積 求め方 高校,